- Yes it does. It is similar to the average atomic mass of Ne on the periodic table. The average atomic mass is in between the given amu values for Ne-20, Ne-21 and Ne-22, and the average amu value calculated is closest to the most abundant isotope, Ne-20.
Source: “Exercise 5.6a” by Jackie MacDonald, licensed under CC BY-SA 4.0.
If you want to review additional examples of how to calculate average atomic mass, Watch How to Calculate Atomic Mass Practice Problems (6 mins 10s)
Video Source: Tyler DeWitt. (2012, October 5). How to calculate Atomic Mass practice problems [Video]. YouTube.
Exercise 5.6b
Calculating Average Atomic Mass
A sample of magnesium is found to contain 78.70% of 24 Mg atoms (mass 23.98 amu), 10.13% of 25 Mg atoms (mass 24.99 amu), and 11.17% of 26 Mg atoms (mass 25.98 amu). Calculate the average mass of a Mg atom.
Check Your Answer [1]
We can also do variations of this type of calculation where you calculate the percent abundance of each isotope, as shown in the next example:
Example 5.6b
Calculating Percent Abundance
Naturally occurring chlorine consists of 35 Cl (mass 34.96885 amu) and 37 Cl (mass 36.96590 amu), with an average mass of 35.453 amu. What is the percent composition of Cl in terms of these two isotopes?
Step 1 – List known quantities and identify what you are asked to find
Known information: 35 Cl (mass 34.96885 amu) and 37 Cl (mass 36.96590 amu), with chlorine having an average atomic mass of 35.453 amu
What am I asked to Find: What is the percent composition of Cl in terms of these two isotopes
Step 2 – Determine how you will solve the problem
Use the following formula to solve problem:
The average mass of chlorine is the fraction that is 35 Cl times the mass of 35 Cl plus the fraction that is 37 Cl times the mass of 37 Cl.
If we let x represent the fraction that is 35 Cl, then the fraction that is 37 Cl is represented by 1.00 − x.
(The fraction that is 35 Cl + the fraction that is 37 Cl must add up to 1, so the fraction of 37 Cl must equal 1.00 − the fraction of 35 Cl.)
Step 3 – Solve the Problem
Substituting this into the average mass equation, we have:
[latex]\begin=<>> l>35.453 \;\text & = (x \times 34.96885 \;\text) + [(1.00 - x) \times 36.96590\;\text] \\[1em] 35.453 & = 34.96885x + 36.96590 - 36.96590x \\[1em] 1.99705x & = 1.513 \\[1em] x & = \frac = 0.7576 \end[/latex]
So solving yields: x = 0.7576, which means that 1.00 − 0.7576 = 0.2424. Therefore, chlorine consists of 75.76% 35 Cl and 24.24% 37 Cl.
Step 4 – Does the answer make sense?
Yes it does. The highest % abundance found is 35 Cl ; which has a mass of 34.96885 amu is closest to the average mass of Cu, which is 35.453 amu.
If you want to watch the full work through of Example 5.6b – Calculation of Percent Abundance, Watch How to Calculate Isotope Abundance (11 mins 48s)
Video Source: DeWitt, T. (2012, October 4). Atomic mass: How to calculate isotope abundance [Video]. YouTube.
Exercise 5.6c
Calculation of Percent Abundance
Naturally occurring copper consists of 63 Cu (mass 62.9296 amu) and 65 Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What is the percent composition of Cu in terms of these two isotopes?
Check Your Answer [2]
Try the interactive learning activity suggested below to reinforce your learning about isotope ratios and atomic mass. Try make mixtures of the main isotopes of the first 18 elements, gain experience with average atomic mass, and check naturally occurring isotope ratios using the Isotopes and Atomic Mass simulation.
Exercise 5.6d
Practice using the following PhET simulation: Isotopes and Atomic Mass
Activity source: Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0
Determining Natural Abundances of Isotopes using Mass Spectrometry.
The occurrence and natural abundances of isotopes can be experimentally determined using an instrument called a mass spectrometer. Mass spectrometry (MS) is widely used in chemistry, forensics, medicine, environmental science, and many other fields to analyze and help identify the substances in a sample of material. In a typical mass spectrometer (Figure 5.6b), the sample is vaporized and exposed to a high-energy electron beam that causes the sample’s atoms (or molecules) to become electrically charged, typically by losing one or more electrons. These cations then pass through a (variable) electric or magnetic field that deflects each cation’s path to an extent that depends on both its mass and charge (similar to how the path of a large steel ball bearing rolling past a magnet is deflected to a lesser extent that that of a small steel BB). The ions are detected, and a plot of the relative number of ions generated versus their mass-to-charge ratios (a mass spectrum) is made. The height of each vertical feature or peak in a mass spectrum is proportional to the fraction of cations with the specified mass-to-charge ratio. Since its initial use during the development of modern atomic theory, MS has evolved to become a powerful tool for chemical analysis in a wide range of applications.
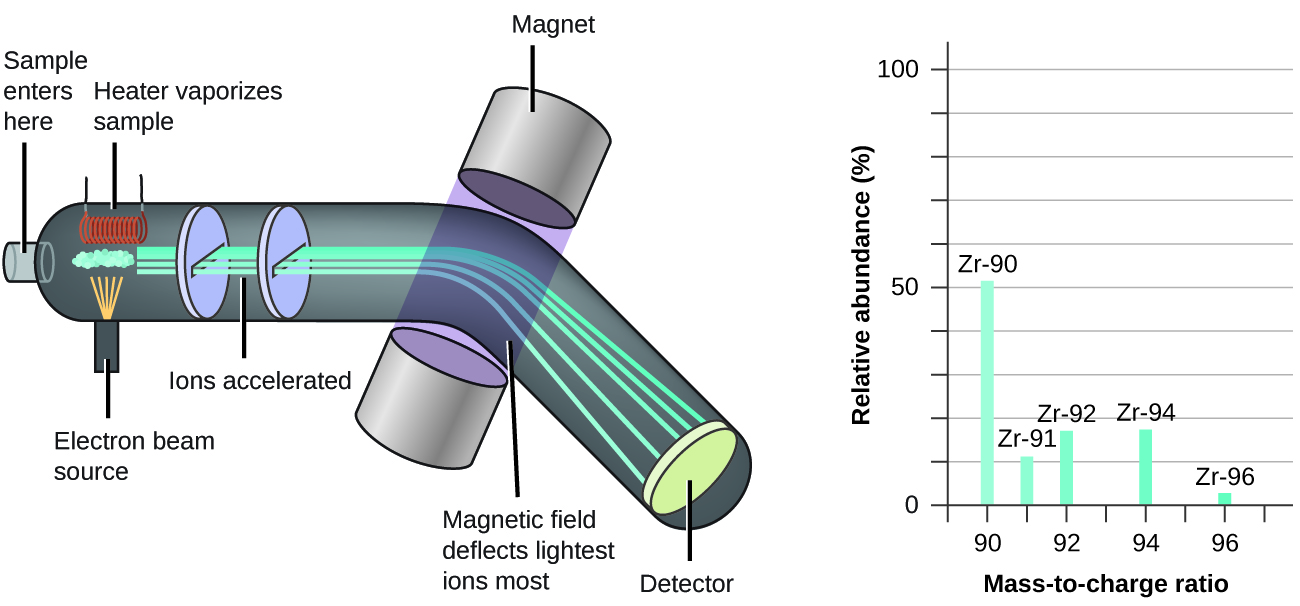 of about 18 percent. Z R 94 has a mass to charge ratio of 94 and a relative abundance of about 18 percent. Z R 96, which has a mass to charge ratio of 96, is the least abundant zirconium isotope with a relative abundance of about 2 percent." width="1300" height="606" />
of about 18 percent. Z R 94 has a mass to charge ratio of 94 and a relative abundance of about 18 percent. Z R 96, which has a mass to charge ratio of 96, is the least abundant zirconium isotope with a relative abundance of about 2 percent." width="1300" height="606" />
Video Source: Bozeman Science. (2013, August 8). Mass spectrometry [Video]. YouTube.
Video Source: Royal Society of Chemistry. (2008, September 27). Mass Spectrometry MS [Video]. YouTube.
Key Equations
- [latex]\displaystyle<> \text = \sum_ (\text \times \text)_i[/latex]
Attribution & References
Except where otherwise noted, this page is adapted from “2.3 – Atomic Structure and Symbolism ” In Chemistry 2e (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson is licensed under CC BY 4.0. Access for free at Chemistry 2e (Open Stax)
- Step 1 - List known quantities and identify what you are asked to find
- Yes it does. It is similar to the average atomic mass of Mg on the periodic table. The average atomic mass is in between the given amu values for Ne-20, Ne-21 and Ne-22, and the average amu value calculated is a bit more than the most abundant isotope, Mg-24.
Known information: 63 Cu (mass 62.9296 amu) and 65 Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What am I asked to Find:What is the percent composition of Cu in terms of these two isotopes? Step 2 - Determine how you will solve the problem Use the following formula to solve problem: The average mass of Copper is the fraction that is 63 Cu times the mass of 63 Cu plus the fraction that is 65 Cu times the mass of 65 Cu
If we let x represent the fraction that is 63 Cu, then the fraction that is 65 Cu is represented by 1.00 − x. (The fraction that is 63 Cu + the fraction that is 65 Cu must add up to 1, so the fraction of 63 Cu must equal 1.00 − the fraction of 65 Cu.) Step 3 - Solve the Problem
[latex]\begin=<>> l>63.546\;\text & = (x \times 62.9296\;\text) + [(1.00 - x) \times 64.9278\;\text] \\[1em] 63.546 & = 62.9296x+ 64.9278 - 64.9278x \\[1em] 1.9982x & = 1.3818\\[1em] x & = \frac = 0.6915\end[/latex]
definition
(also, unified atomic mass unit, u, or Dalton, Da) unit of mass equal to 1/12 the mass of a 12C atom
× Close definition
(also called the elementary charge) equals the magnitude of the charge of an electron (e) with e = 1.602 × 10−19 C
× Close definition
alternative unit equivalent to the atomic mass unit
× Close definition
alternative unit equivalent to the atomic mass unit
× Close definition
average mass of atoms of an element, expressed in amu
× Close definition
License
Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

 center of the atom and is 10 to the negative fifteenth power meters. The central figure shows a photograph of an American football stadium. The figure on the right shows a photograph of a person with a handful of blueberries." width="1300" height="400" />
center of the atom and is 10 to the negative fifteenth power meters. The central figure shows a photograph of an American football stadium. The figure on the right shows a photograph of a person with a handful of blueberries." width="1300" height="400" /> of about 18 percent. Z R 94 has a mass to charge ratio of 94 and a relative abundance
of about 18 percent. Z R 94 has a mass to charge ratio of 94 and a relative abundance